[Algorithm] recursion - 재귀 관련 예제, 관련 문제

상태공간트리를 탐색하는 재귀함수를 생각해보자

recursion을 짤 때는 breakpoint를 만들고, 그 값을 감소시키면서 자기 자신을 다시 실행시키는 방식으로 코드를 작성해야한다.

 

따라서 재귀 함수에는 적어도 하나의 recursion에 빠지지 않는 경우가 존재해야하고, recursion case를 계속 반복하다보면 결국 base case로 수렴해야된다. 그렇지 않으면 계속 실행되다가 stackoverflow가 발생한다. 

 

모든 recursion은 iteration으로 변경이 가능하고 그 역도 가능하다. 그래도 recursion을 쓰면 복잡한 코드를 좀 더 간결하게 표현 할 수 있다. 다만 매개변수 전달할때나 액티베이션 프레임 생성 등에 오버헤드가 있다. 

 

알고리즘 문제를 풀다보면 사이즈가 큰 배열이나 리스트 매개변수를 전달하는 부분 때문에 오버헤드가 발생해서 시간초과 등이 발생할 때가 가끔씩 있었다. 그래서 배열 같은 경우에는 항상 전역 변수로 만들어서 사용한다.

public static double power(double x, int n){
	if(n ==0) return 1; // base case
	else return x*power(x, n-1); // recursion case
}

// x^0 = 1, x^n = x*x^(n-1) if n>0

 

 

int search(int[] data, int n , int target){
	for(int i = 0; i<n; i++)
		if(data[i] == target) return i;
	return -1;
} // 순차탐색의 예시. data[0]에서 data[n-1] 사이에서 target을 검색하는 것.
// 하지만 검색 구간의 시작인덱스 0은 보통 생략한다. 이 것이 암시적 파라미터.
// 데이터의 시작지점이 explicit 파라미터로 바꿔줘야.

재귀함수를 짤 때는 implicit 한 파라미터를 explicit 파라미터로 바꿔야 좋다. 검색 index의 범위가 보다 명확해지고, 범위 지정이 가능해졌다.

int search(int[] data, int begin, int end, int target){
	if(begin > end) return -1; // 파라미터에서 end를 생략한다면 대신 data.length()를 이용
	else if(target == data[begin]) return begin;
	else return search(data, begin+1, end, target)
}
// data[begin]에서 data[end] 사이에서 target을 검색함. 즉 검색구간의 시작점을 명시적으로 지정함.

search(data, 0, n-1, target); 

하지만 이 부분을 생각해내는 것은 생각보다 많은 연습이 필요한 것 같다. 

 

int findMax(int[] data, int begin, int end){ // 데이터는 1개 이상
	if(begin == end) return data[begin];
	else return Math.max(data[begin], findMax(data, begin+1, end));
} // begin~end 사이에서 최대값을 찾아 반환한다. 
// 최대값찾기1

int findMax(int[] data, int begin, int end){
	if(begin == end) return data[begin];
	else {
		int middle = (begin+end)/2;
		int max1 = findMax(data,begin, middle);
		int max = findMax(data, middle+1, end);
		return Math.max(max1, max2);
	}
} // 최대값찾기2

public static int binarySearch(String[] items, string target, int begin, int end){
	if(begin > end) return -1;
	else {
		int middle = (begin+end)/2;
		int compResult = target.compareTo(items[middle]);
		if(compResult == 0) return middle;
		else if(compResult < 0)
			return binarySearch(items, target, begin, middle-1);
		else
			return binarySearch(items, target, middle+1, end);
	}
}

binarySearch(data, target, 0, n-1);

 

만약 현재 위치에서 출구까지 가는 경로를 찾는 미로 문제를 recursion 함수로 구현해본다 가정했을 때

이 함수의 base case는 2가지이다.

1. 현재 위치가 출구이거나

2. 이웃한 셀들 중 하나에서 현재 위치를 지나지 않고 출구까지 가는 경로가 있거나

boolean findPath(x,y)
	if(x,y) is either on the wall or a visited cell
		return false
	if (x,y) is the exit
		return true;
	else
		mark (x,y) as a visited cell // 중복 방문을 막기 위해서 마킹
		for each neighbouring cell (x', y') of (x,y) do
				if findPath(x', y')
					return true;
		return false; 

이를 자바로 구현하면 다음과 같다

public class maze {
	private static int n = 8;
	private static int[][] maze ={
		{0,0,0,0,0,0,0,1},
		{0,1,1,0,1,1,0,1},
		{0,0,0,1,0,0,0,1},
		{0,1,0,0,1,1,0,0},
		{0,1,1,1,0,0,1,1},
		{0,1,0,0,0,1,0,1},
		{0,0,0,1,0,0,0,1},
		{0,1,1,1,0,1,0,0}
	}

	private static final int PATHWAY_COLOR = 0;
	private static final int WALL_COLOR = 1;
	private static final int BLOCKED_COLOR = 2;
	private static finsal int PATH_COLOR = 3;
	
	// 종료조건 1. 그리드 밖, 2. 길이 아님 3. exit 지점에 도달
	public static boolean findMazePath(int x, int y){
		if(x < 0 || y < 0 || x >=n || y>=n) // n*n 그리드 내에 있는가(index 0~n-1)
			return false;
		else if (maze[x][y] != PATHWAY_COLOR) // 길이 아니면 무조건 false
			return false;
		else if(x == n-1 && && y == n-1) { // exit 지점에 도달
			maze[x][y] == PATH_COLOR;
			return true;
		} 
		else {
			maze[x][y] = true;
			if(findMazePath(x-1, y) || findMazePath(x, y+1) 
			|| findMazePath(x+1,y) || findMazePath(x, y-1)) {// 모든 방향을 찾아봄. recursion
				return true; // 길이 있으면 true
			}
			maze[x][y] = BLOCKED_COLOR; // 길이 없음
			return false; // 길이 아니여서 되돌아나옴
		}
	}

	public static void main(String[] args){
		printMaze();
		findMazePath(0,0);
		printMaze();
	}
}

recursion이 데이터를 변경할 때에는 조심해야한다. 호출 전,후에 기존의 데이터가 변경되지 않고 유지되도록 하는 것이 좋은데, powerset이라는 이름이 더 편한 멱집합의 예시를 보면 알 수 있다.

powerSet(P, S) // S의 멱집합을 구한 후 각각에 집합 P를 합집합하여 출력하라
	if S is an empty set
		print p
	else
		let t be the first element of s;
		powerSet(p, s-{t}); // t포함 하지 않는 부분집합
		powerSet(pu{t}, s-{t}); // t를 반드시 포함하는 부분집합

// recursion 함수가 두 개의 짛밥을 매개변수로 받도록 설계해야함.
// 두 번째 집합의 모든 부분집합들에 첫번째 집합을 합집합 하여 출력한다

```java
private static char data[] = {'a','b','c','d','e','f'};
private static int n = data.length;
private static boolean[] include = new boolean[n]; // 트리 상의 나의 위치 표현

public static void powerSet(int k){  // k, include는 트리 상의 나의 위치 표현
	// data[k],~data[n-1]의 멱집합을 구한 후
	// 각각에 include[i]=true, i=0, ... k-1인 원소를 추가하여 출력하라
	if(k==n) { // base case는 k가 n. 집합s가 공집합이라는 뜻. 내 위치가 leaf라면
	//print data
		for(int i = 0; i<n; i++){
			if(include[i]) system.out.print(data[i] + " ");
			System.out.println();
		}
		return;
	}
	include[k] = false;
	powerSet(k+1); // data[k]를 포함하지 않는 경우. 먼저 왼쪽으로 내려간다
	include[k] = true;
	powerSet(k+1); // data[k]를 포함하는 경우. 이번에는 오른쪽으로 내려간다
} // 이 함수를 처음 호출할 때는 powerSet(0) 호출로 시작함. (P는 공집합, S는 전체집합)
```

모든 가능한 순열을 프린트하는 문제도 마찬가지로 다음 재귀 실행시 기존의 데이터가 변경되어서 이후 다른 리턴값이 나오지 않도록 한번 변경된 데이터를 다시 원래대로 바꿔준다

// S의 모든 순열들을 생성한 후 각각에 prefix string을 앞에 붙여서 출력한다
void printPermu(a prefix string, a set S){
	if |S| is 0
		print the prefix string;
	else
		for each element x in S
			printPerm(the prefix string + x, S-{x});
}

char data[] = {'a','b','c','d'};
int n = 4;

void permu(int k){
	if(k == n) {
		print data[0...n-1];
		return;
	}
	for(int i = k; i<n; i++){
		swap(data, k, i); // data[k]와 data[i] 스왑해서 
		perm(k+1);
		swap(data, k, i)
	}
}
// data[0..k-1]을 prefix로 하고, data[k..n]으로 만들 수 있는 모든 순열을
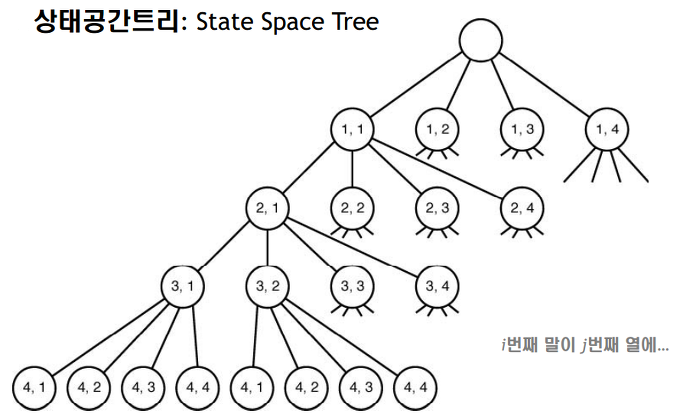
// 프린트 하되, 배열 data에 저장된 값들의 순서는 그대로 유지한다

미로 문제 외에도 재귀만을 이용해서 풀 수 있는 문제 중 유명한 문제로는 재귀를 이용한 백트래킹 문제인 n-queens 문제, 멱집합 문제, 수열문제 등이 있고 이를 이용해서 knapsack(배낭) 문제, TSP(외판원)문제 등을 풀어낼 수 있다. 

재귀를 이용해서 그래프 탐색방식인 DFS를 구현 할 수 있다. 물론 stack을 이용해서도 구현할 수 있지만 일반적인 PS에서는 재귀방식으로 짜는 것이 더 수월해서 많이 사용한다고 한다. 

https://www.acmicpc.net/problem/9663 n-queens

https://www.acmicpc.net/problem/12865 배낭문제

https://www.acmicpc.net/problem/10971 외판원문제

https://www.acmicpc.net/problem/11729 하노이탑 문제

 

귀납적인 사고로 생각하는 것이 중요하다. 함수의 형태를 잡고, 함수의 인자는 어떤걸 받을지, 어디까지 계산하고 자기 자신에게 다시 넘겨줄지에 대한 생각을 하면서 작성해야한다.